|
|
Derivation
The following demonstrates the derivation of the equation for the
payment of a loan.
Here are the definitions of the key variables used.

First, we illustrate the principal amount after each of the payments. Each payment is
made up of the interest part and the principal part. When each payment is made, the
ending principal is equal to the beginning principal minus the principal part of the payment.

There are n payments. We number the payments from 0 to n-1. After the payment numbered n-1,
the principal is zero.
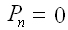
The payment amount is composed of a principal part and and interest part. The interest part of the
payment is determined by taking the annual interest rate, dividing it
by the number of payments per year and the multiplying that value by the principal.

Using this expression, we can solve for the principal value of the payment.

We can now express the principal after the k-th payment in terms of the whole payment value. I introduce
a new term m to help keep the equations simple.
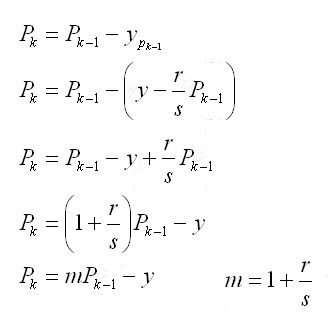
Now we can begin solving the recurrence relation. We want to find the value for y.
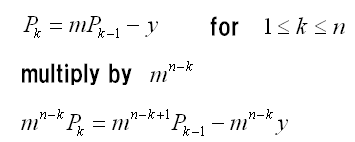
To simplify the solution, we write out the values for k = 1, 2, 3 ... n-1, n-1, n.
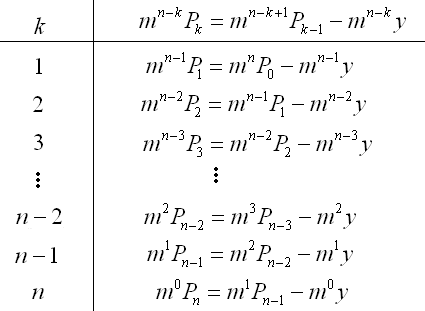
Sum the terms on each side of the = sign. Cancel terms in the process.
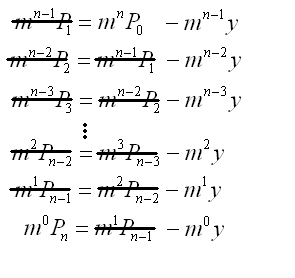
The sum is now just a geometric sequence.
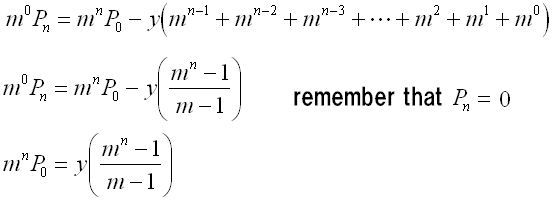
Do some algebra and solve for y.

The final result is
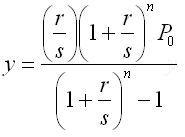
|
|
|