|
|
L'Hopital's rule
Fun with L'Hopital's rule: Converting a geometric series to an arithmetic series
I'm bored tonight so I thought I would add this little trick to the web.
I was always intrigued with L'Hopital's Rule.
However, it was not very
much fun until I found a few uses for it. While playing with the arithmetic series
and geometric series, I found a way to relate the two by using L'Hopital's Rule.
First we state the very well known closed formula for a geometric series.

Next, we take the derivative of the statement.

The right-hand side becomes

So, now it looks like we have a very convenient close formula for the summation f'(x).
Let's try to find f'(1):


We have a problem. Thanks to L'Hopital we can resolve this issue. We will
have to apply L'Hopital's rule twice.
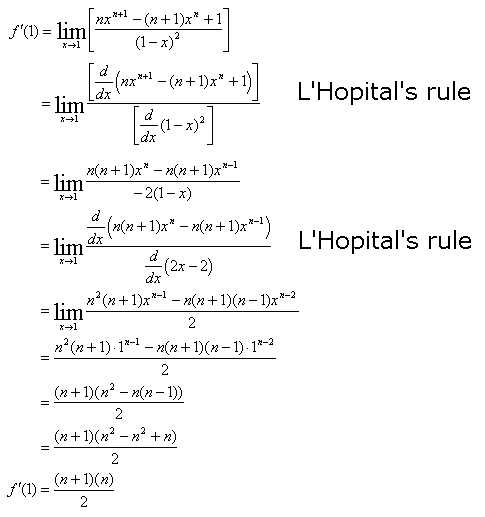
This is a more complex example. We will use our basic geometric series again.

We will take some derivatives and do some multiplication to create a neat series.


Setting x=1, we have a neat looking series. However, the close form of g(x) is rather ugly.
But, we do know that it has a (1-x)^4 in the denominator, so setting x=1 will not work. We
can use L'Hoptile's rule again... well, 4 times.

To do the derivative by had would take a while and would be quite ugly. Maple makes this
much easier. Here is the maple code:
f := proc (x) options operator, arrow; (1-x^(n+1))/(1-x) end proc;
g := diff(diff(x*(diff(f(x), x)), x), x);
g:=simplify(g);
a := numer(g);
b:=denom(g);
a:=diff(a,x);
a:=diff(a,x);
a:=diff(a,x);
a:=diff(a,x);
b:=diff(b,x);
b:=diff(b,x);
b:=diff(b,x);
b:=diff(b,x);
g:=a/b;
x:=1;
g:=simplify(g);
|
Now we have our clean, little result for g(1):


Well, it has been fun. Until I get bored again.
|
|