|
|
Fraction e^x
Converting a Power Series to a Continued Fraction
with e^x as an Example
Iteration Process
e^x example
Back in 1989 or 1990, I started playing around with continued fractions. I was bored and decided
to try to convert e^x from a power series to a continued fraction. I came to a very neat solution.
I then tried to formalize a way to convert any power series to a continued fraction. After having
about 15 sheets of paper with scribbles all over the place, I decided I had not been that bored.
About five years later, I discovered Maple. I put in the general power
series and wrote a couple of little
Maple procedure. In less than a minute, I saw what had taken days to do by hand. I also found that
many determinants lived inside this continued fraction. The following is a summary of what I found.
I have looked around the net for this fraction and have not seen it yet, so I thought I would
put this web page out there. If you have any further information about this fraction, please send
me an email, rollins@wfu.edu.
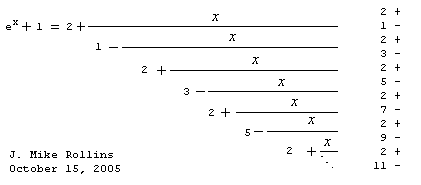
Iteration 1
Begin with a basic power series.
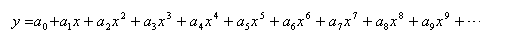
Factor out x from the second term to infinity.
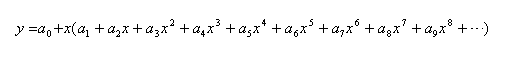
Convert the parenthesized expression to a fraction.
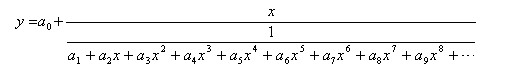
Expand the denominator by performing long division.
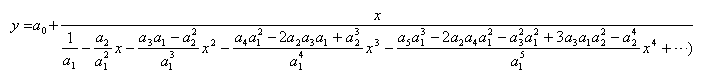
Iteration 2
Next, factor out x from the series as we did before.
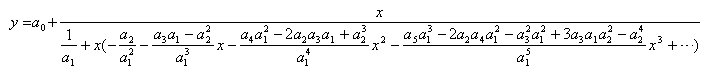
Convert the series to a fraction.
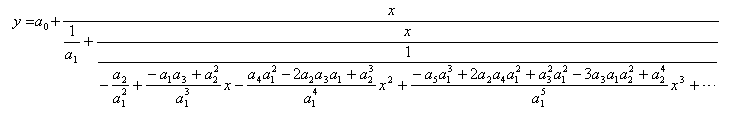
Expand the denominator by long division again.
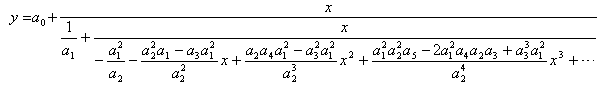
Iteration 3
This is starting to get a little ugly. So, let's not do iteration 3.
So, I will just jump to the interesting part.
The Pattern
click here for a more general description
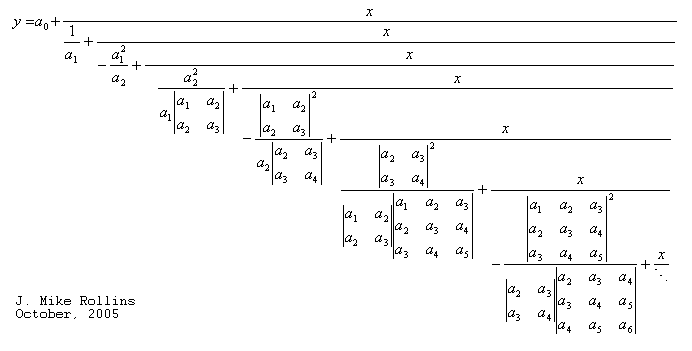
A very elegant fraction can be derived for e to the x power.
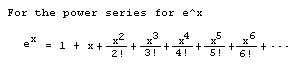
Assign values for a0,a1,a2 ...

Next, we can evaluate the messy fractions of determinants.
I used Maple to evaluate these determinants. It gets really messy.
|
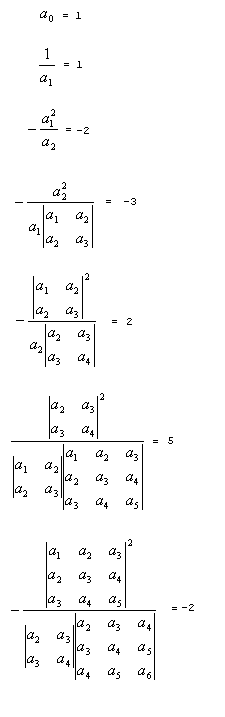
|
Now we can create our continued fraction with these values.

|
In this final step, I move the negative sign around so that
the fraction has an alternation between + and -. I also have
added 1 to both sides so that the value of 2 is also alternating.
|
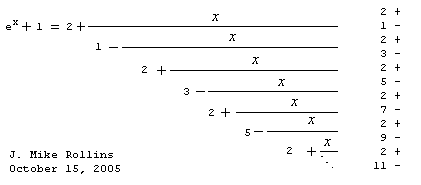
|
|
|
|